1 Armatures longitudinales

1.1 Sections à respecter

1.1.1 Section minimale

Conformément à l’Eurocode 2 et à son annexe française, la section $A_s$ des armatures longitudinales doit être telle que :

\[ A_s\geq max\left[A_{s,min1};A_{s,min2}\right] \]

$A_{s,min1}$ est la section minimale nécessaire pour la maîtrise de la fissuration.

\[ A_{s,min1}=0.26b_wdf_{ctm}/f_{yk} \]

$A_{s,min2}$ correspond à la condition de non-fragilité :

\[ A_{s,min2}=0.0013b_td \]

Dans le cas particulier des pieux, la norme NF P94-262 (tableau Q.3.4.2.2) préconise une armature longitudinale en fonction de la section transversale du pieu ($A_c$) :

Si la section $A_c\leq0.5m²$, alors $A_{s,min}=0.005A_c$
Si la section $0.5m²\leq A_c\leq1.0m²$, alors $A_{s,min}\geq0.0025m²$
Si la section $A_c>1.0m²$, alors $A_{s,min}=0.0025A_c$

1.1.2 Section maximale

La section d’armatures longitudinales ne doit pas dépasser, en dehors de zones de recouvrement, la valeur maximale autorisée par l’Eurocode 2 : \[ A_{s,max}=0.04A_c \]

1.2 Longueur d’ancrage d’une barre longitudinale

Contrainte ultime d’adhérence entre la barre d’acier et le béton \[ f_{bd}=2.25\eta_1\eta_2f_{ctd} \]
- $f_{ctd}$ Résistance du béton en traction (MPa) (sa valeur dépend de la situation)
- $\eta_1$ Conditions d’adhérence réputées bonnes = 1.0 // médiocres = 0.7
- $\eta_2$ Paramètre qui dépend du diamètre de la barre
  - Si $\phi_n\leq32mm\rightarrow\eta_2=1.0$
  - Si $\phi_n>32mm\rightarrow\eta_2=(132-\phi_n)/100$ ($\phi_n$ en mm)
Longueur d’ancrage de référence: il s’agit de la longueur $l_{b,rqd}$nécessaire pour ancrer la force $A_s\sigma_{sd}$ qui règne dans une barre droite sous la contrainte d’adhérence $f_{bd}$ supposée constante.

\[ l_{b,rqd}=\frac{\phi_n}4\frac{\sigma_{sd}}{f_{bd}} \]

où $\sigma_{sd}$ est la contrainte de calcul de la barre dans la section à partir de laquelle on mesure l’ancrage \[ \sigma_{sd}=\frac{f_{yk}}{\gamma_s} \] où $\gamma_s$ est pris de l’ELU Fondamental

Longueur d’ancrage

\[ l_{bd}=\alpha_1\alpha_2\alpha_3\alpha_4\alpha_5l_{b,rqd} \]

Coefficient	Description
$\alpha_1=1.0$	Facteur d’influence dû à la forme des barres (ancrage droit)
$\alpha_2=1-0.15\frac{c_d-\phi_n}{\phi_n}$	Facteur d’influence dû à l’enrobage (ancrage droit) $0.7\leq\alpha_2\leq1.0$ avec $c_d=min\left(c,\;\frac a2\right)$ où $c$ est l’enrobage de la barre longitudinal et $a$ est la distance entre nus des barres longitudinales
$\alpha_3=1$	Facteur d’influence dû au confinement par des armatures transversales non soudées aux armatures longitudinales
$\alpha_4=0.7$	Facteur d’influence dû au confinement par des armatures transvesales soudées
$\alpha_5=1$	Facteur d’influence dû au confinement par compression transversale

Condition à garantir: $\alpha_2\alpha_3\alpha_5\geq0.7$

Longueur d’ancrage minimale \[ l_{bd,min}=max\left(0.6l_{b,rqd};10\phi_n;100mm\right) \]

Hypothèse défavorable : barre comprimée

Finalement, la valeur de la longueur d’ancrage à retenir pour une barre est : \[ l_{bd}=max\left(l_{bd};l_{bd,min}\right) \]

1.3 Longueur de recouvrement

Ce calcul utilise les coefficients $ _1, _2, _3, _4, _5 $ déjà calculés précédemment pour la longueur d’ancrage.

On rajoute : $\alpha_6=1.5$

Longueur de recouvrement: \[ l_0=\alpha_1\alpha_2\alpha_3\alpha_4\alpha_5\alpha_6l_{b,rqd} \] Longueur de recouvremen minimale: \[ l_{0,min}=max\left[0.3\alpha_6l_{b,rqd};15\phi_n;200mm\right] \]

1.4 Longueur de décalage des courbes de moments fléchissants

Calcul du bras de lévier: \[ z=0.9d=0.9\left(h-z_{G}\right) \]

h: épaisseur de la paroi

$z_G$: centre de gravité des armatures tendues
Calcul de la longueur de décalage à considérer: \[ a_l=\frac z2cot\theta \]

$\theta$ : inclinaison des bielles de béton ($1\leq cot \theta \leq 2.5$)

1.5 Mise en place des barres d’acier

Quelques règles à respecter:

3 barres au maximum dans un groupe de barres
100 mm d’écartement entre nu de barres longitudinales (80 mm en zone de recouvrement)
Il est préférable garder un espacement régulier entre barres longitudinales pour faciliter la construction et le façonnage de la cage.
La distribution globale des barres au sein d’une cage ne doit pas mettre en cause le transport et le levage.

2 Armatures transversales

2.1 Section minimale

Le pourcentage d’armatures transversales se calcule comme suit : \[ \rho_w=\frac{A_{sw}}{sb_w\sin\alpha} \]

$A_{sw}$ est la section d’armatures transversales à une section donnée
$s$ est l’espacement des armatures transversales
$b_w$ est la largeur de la section
$\alpha$ est l’inclinaison des armatures transversales par rapport aux armatures longitudinales.

Même lorsqu’aucune armatures d’effort tranchant n’est requise, un ferraillage transversal minimal est à prévoir. \[ \rho_{w,min}=0.08\frac{\sqrt{f_{ck}}}{f_{yk}} \]

2.2 Façonnage des aciers transversaux

Plusieurs types des aciers transversaux existe:

Grands cadres: il englobent l’ensemble de barre longitudinales (elles sont soudées sur eux)
Petits cadres: ils permettent le cheminement des efforts transversaux à l’intérieur de la paroi.
Etriers: barres à 2 brins reliant 2 groupes de barres longitudinales mises une en face de l’autre
Epingles: barres à 1 brin reliant 2 groupes de barres longitudinales mises une en face de l’autre

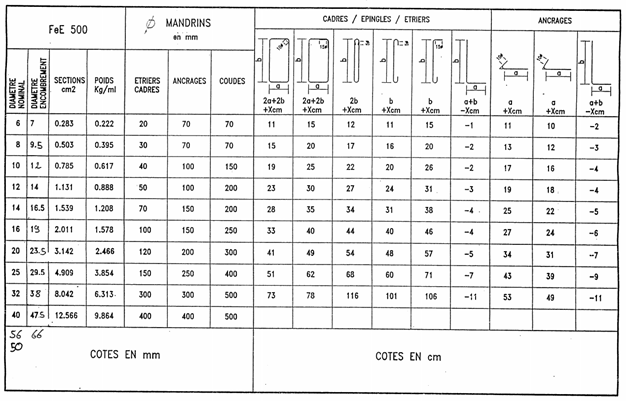
Sur-longueur à prévoir pour garantir les longueurs de mise en charge (fonction du diamètre de la barre) :

Dispositions constructives