Matériaux
1 Béton
1.1 Loi de comportement
La loi de comportement du béton est de type élastoplastique (parabole-rectangle). \[ \begin{array}{cc}\sigma_c=f_{cd}\left[1-\left(1-\frac{\displaystyle\varepsilon_c}{\displaystyle\varepsilon_{c2}}\right)^n\right]&\;0\leq\varepsilon_c\leq\varepsilon_{c2}\\\sigma_c=f_{cd}&\varepsilon_{c2}\leq\varepsilon_c\leq\varepsilon_{cu2}\end{array} \]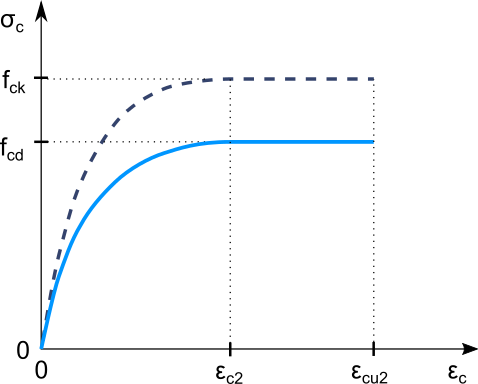
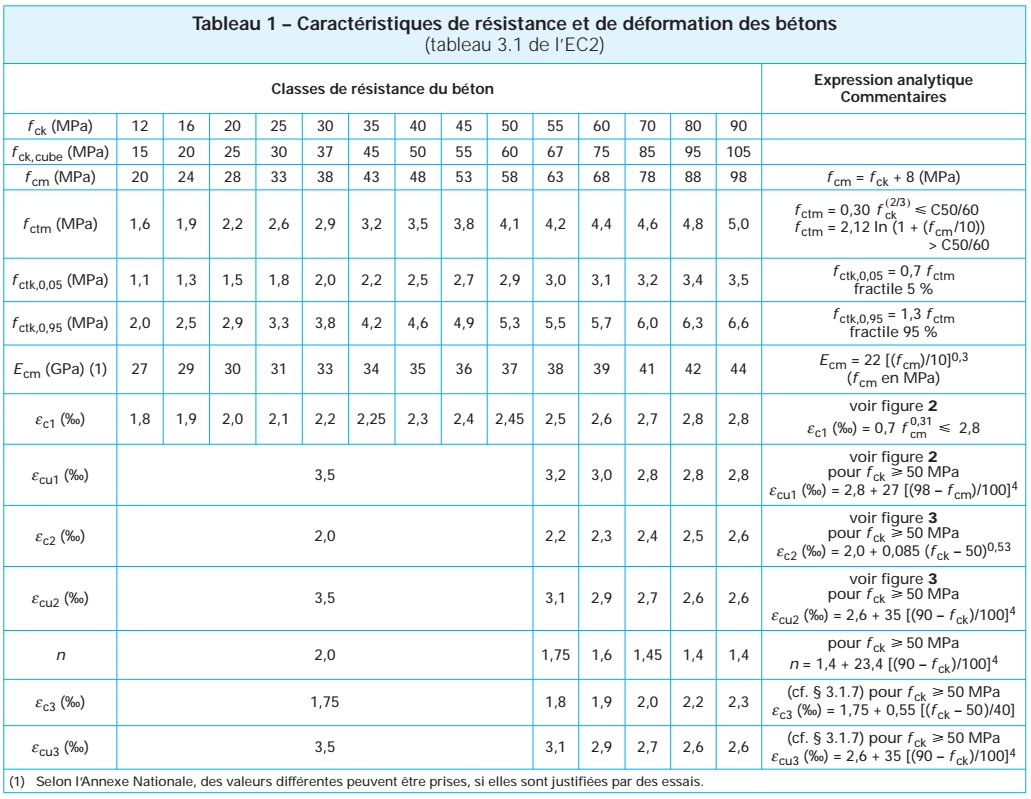
1.2 Contraintes admissibles et facteurs de sécurité
1.2.1 Annexe nationale français (NF P94-282)
Dans ce chapitre, nous fournissons un calcul de contraintes admissibles pour un béton C30/37, conformément à la NF P94-282 §6.4.
Contrainte admissible de compression du béton (valeur caractéristique à 28 jours) : \[ f_{ck}=30MPa \] Résistance caractéristique à la compression à la mise en œuvre (Table 6.4.1.1) : \[ C_{max}=35MPa \] Coefficients empiriques (Table 6.4.1.1) : \[ k_1=1.30 \]
\[ k_2=1.05 \]
Nous considérons l’absence de contrôle renforcé (Table 6.4.1.1), par conséquent : \[ k_3=1.00 \] Résistance caractéristique à la compression : \[ f_{ck}^\ast=\frac{min\left(f_{ck},C_{max}\right)}{k_1k_2}=21.98MPa \]
Conformément à la NF P94-282 §6.4.2 (7) Note 1, \(f_{ck}^\ast\) ne doit être utilisée que pour les vérifications de la résistance à la compression du béton.
Résistance moyenne à la compression : \[ f_{cm}=f_{ck}+8MPa\;=38MPa \] Résistance moyenne à la traction : \[ f_{ctm}=0.3f_{ck}^{2/3}\;=2.90MPa \] Contrainte admissible en traction, valeur caractéristique (5%) : \[ f_{ct;k;0.05}=0.7f_{ctm}\;=2.03MPa \] Contraintes admissibles à l’ELS (NF P94-282 §6.4.1 (8)):
- Compression moyenne :
\[ \sigma_{c,mean}=0.3k_3f_{ck}^\ast=6.6MPa \]
- Compression maximale :
\[ \sigma_{c,max}=0.6\cdot min\left(k_3f_{ck}^\ast;f_{ck}\right)=13.2MPa \]
Résistances de calcul à l’ELU (Eurocode 2 §3.1.6) :
\(\alpha_{cc}=1.0\), \(\alpha_{ct}=1.0\), \(\gamma_c=1.5\)
- Compression :
\[ f_{cd}=\alpha_{cc}\frac{min\left(k_3f_{ck}^\ast;C_{max}\right)}{\gamma_c}=14.7MPa \]
- Traction :
\[ f_{ctd}=\alpha_{ct}\frac{f_{ctk,0.05}}{\gamma_c}=1.35MPa \]
Résistances de calcul à l’ELU Accidentel (Eurocode 2 §3.1.6) :
\(\alpha_{cc}=1.0\), \(\alpha_{ct}=1.0\), \(\gamma_c=1.2\)
- Compression :
\[ f_{cd}=\alpha_{cc}\frac{min\left(k_3f_{ck}^\ast;C_{max}\right)}{\gamma_c}=18.3MPa \]
- Traction :
\[ f_{ctd}=\alpha_{ct}\frac{f_{ctk,0.05}}{\gamma_c}=1.7MPa \]
1.2.2 Annexe nationale belge
Dans ce chapitre, nous fournissons un calcul de contraintes admissibles pour un béton C30/37, conformément à l’annexe nationale belge (BNA).
Contrainte admissible de compression du béton (valeur caractéristique à 28 jours) : \[ f_{ck}=30MPa \] Résistance caractéristique à la compression à la mise en œuvre (Table 6.4.1.1) : \[ C_{max}=35MPa \] Coefficients empiriques (BNA §2.4.2.5 (2)) : \[ k_f=1.1 \] Nous considérons l’absence de contrôle renforcé, par conséquent : \[ k_3=1.0 \] Résistance moyenne à la compression : \[ f_{ck}^\ast=\frac{min\left(f_{ck},C_{max}\right)}{k_f}=27.27MPa \] Résistance moyenne à la compression : \[ f_{cm}=f_{ck}+8MPa\;=38MPa \] Résistance moyenne à la traction : \[ f_{ctm}=0.3f_{ck}^{2/3}\;=2.90MPa \] Contrainte admissible en traction, valeur caractéristique (5%) : \[ f_{ct;k;0.05}=0.7f_{ctm}\;=2.03MPa \] Contraintes admissibles à l’ELS :
- Compression moyenne :
\[ \sigma_{c,mean}=0.3k_3f_{ck}^\ast=8.2MPa \]
- Compression maximale :
\[ \sigma_{c,max}=0.6\cdot min\left(k_3f_{ck}^\ast;f_{ck}\right)=16.4MPa \]
Résistances de calcul à l’ELU (Eurocode 2 §3.1.6) :
\(\alpha_{cc}=0.85\), \(\alpha_{ct}=1.0\), \(\gamma_c=1.5\)
- Compression :
\[ f_{cd}=\alpha_{cc}\frac{min\left(k_3f_{ck}^\ast;C_{max}\right)}{\gamma_c}=15.5MPa \]
- Traction :
\[ f_{ctd}=\alpha_{ct}\frac{f_{ctk,0.05}}{\gamma_c}=1.35MPa \]
Résistances de calcul à l’ELU Accidentel (Eurocode 2 §3.1.6) :
\(\alpha_{cc}=0.85\), \(\alpha_{ct}=1.0\), \(\gamma_c=1.2\)
- Compression :
\[ f_{cd}=\alpha_{cc}\frac{min\left(k_3f_{ck}^\ast;C_{max}\right)}{\gamma_c}=19.3MPa \]
- Traction :
\[ f_{ctd}=\alpha_{ct}\frac{f_{ctk,0.05}}{\gamma_c}=1.7MPa \]
2 Acier
2.1 Loi de comportement
La loi de comportement de l’acier est de type élastoplastique.
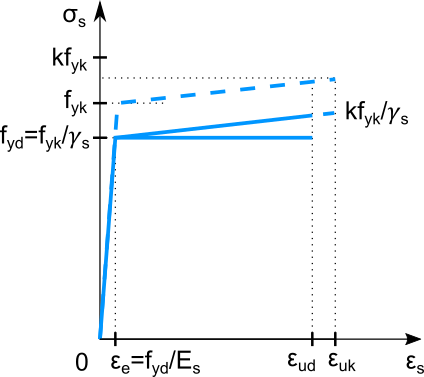
L’Eurocode 2, suivant la normale EN 10080, définit trois clases de ductilité :
- Classe A : ductilité normale (treillis soudés formés à froid)
\[ \sigma_s=432.71+952.38\varepsilon_S≯454MPa \]
- Classe B : haute ductilité (barres HA laminées à chaud)
\[ σ_s=433.20+727.27ε_S≯466MPa \]
- Classe C : très haute ductilité (aciers réservés à des usages spéciaux; constructions parasismiques)
\[ σ_s=432.84+895.52ε_S≯493MPa \]
L’annexe nationale fournir le rapport entre la valeur ultime et la valeur caractéristique de la déformation de l’acier:
| Annexe nationale | \(\varepsilon_{ud} / \varepsilon_{uk}\) |
|---|---|
| Française | 0.9 |
| Belge | 0.8 |
Par exemple, conformément à l’annexe française :
| Ductilité | \(\varepsilon_{ud}\) | \(\varepsilon_{uk}\) |
|---|---|---|
| A | 22.5 ‰ | 25 ‰ |
| B | 45 ‰ | 50 ‰ |
| C | 67.5 ‰ | 75 ‰ |
La déformation ultime de la zone élastique (\(\varepsilon_e\)) dépend en toute règle de la combinaison de calcul considérée. Dans le cas d’une combinaison à l’ELU (durable ou transitoire): \[ f_{yd}=\frac{f_{yk}}{\gamma_s}=\frac{500MPa}{1.15}=435MPa \]
\[ E_s=200000MPa \]
\[ \varepsilon_e=\frac{f_{yd}}{E_s}=\frac{435MPa}{200000MPa}=2.175‰ \]
3 Notations
3.1 Contraintes
| Symbol | Unité | Description |
|---|---|---|
| \(f_{ck}\) | MPa | Contrainte admissible de compression du béton (valeur caractéristique à 28 jours) |
| \(C_{max}\) | MPa | Résistance caractéristique à la compression à la mise en œuvre |
| \(k_1\) | - | Coefficient empirique tenant compte du mode de mise en place dans le sol |
| \(k_2\) | - | Coefficient empirique tenant compte des difficultés de bétonnage liées à la géométrie de la structure |
| \(k_3\) | - | Coefficient empirique tenant compte des contrôles d’intégrité effectués |
| \(f_{ck}^*\) | MPa | Résistance caractéristique à la compression à considérer dans les calculs de fondations et écrans de soutènement |
| \(f_{cm}\) | MPa | Contrainte admissible de compression moyenne |
| \(f_{ctm}\) | MPa | Contrainte admissible de compression maximale |
| \(f_{ct;k;0.05}\) | MPa | Contrainte admissible en traction, valeur caractéristique (5%) |
| \(f_{cd}\) | MPa | Contrainte admissible de compression du béton (valeur de calcul) |
| \(\alpha_{cc}\) | - | Coefficient tenant compte des effets à long terme sur la résistance en compression du béton > Annexe nationale française = 1.0 > Annexe nationale belge = 0.85 |
| \(\alpha_{ct}\) | - | Coefficient tenant compte des effets à long terme sur la résistance en traction du béton > Annexe nationale française = 1.0 > Annexe nationale belge = 1.0 |
| \(f_{yd}\) | MPa | Contrainte admissible de l’acier (valeur de calcul) |
| \(f_{yk}\) | MPa | Contrainte admissible de l’acier (valeur caractéristique) |
| \(\gamma_c\) | - | Coefficient partiel sur la résistance du béton |
