Analyse à l’ELS
1 Introduction
Ce document détaille comment l’analyse à l’ELS est mené pour les sections circulaires et pour les sections rectangulaires en béton armé.
2 Section circulaire
Ce chapitre détaille le calcul d’une section circulaire en béton armé soumise à la flexion déviée (ELS).
2.1 Notations
2.1.2 Efforts
| Symbol | Unité | Description |
|---|---|---|
| \(N\) | MN | Effort normal appliqué au centre de gravité de la section |
| \(M\) | MNm | Moment fléchissant appliqué au centre de gravité de la section |
2.1.3 Contraintes
| Symbol | Unité | Description |
|---|---|---|
| \(\sigma_{s}\) | MPa | Contrainte dans les aciers |
| \(\sigma_c\) | MPa | Contrainte de compression dans le béton |
| \(f_{ck}\) | MPa | Contrainte admissible de compression du béton (valeur caractéristique) |
| \(f_{yd}\) | MPa | Contrainte admissible de l’acier (valeur de calcul) |
| \(f_{yk}\) | MPa | Contrainte admissible de l’acier (valeur caractéristique) |
2.2 Principe de calcul à l’ELS
2.2.1 Hypothèses de calcul
Le calcul à l’ELS des sections en béton armé tient en compte des hypothèses suivantes :
- Hypothèse 1 : La résistance à la traction du béton est négligée.
- Hypothèse 2 : La résistance à la compression du béton est limitée à la contrainte admissible \(\overline{\sigma_c}\) à l’ELS.
- Hypothèse 3 : La résistance à la traction de l’acier est limitée à la contrainte admissible \(\overline{\sigma_s}\) à l’ELS.
Les lois de comportement du béton et de l’acier sont fournies dans le chapitre Matériaux de ce manuel.
2.2.2 Vérification de la section béton armé à l’ELS
La vérification de la section béton armé à l’ELS se réalise en homogénéisant la section afin de prendre en compte la présence de deux matériaux de rigidités différentes. L’équilibre de la section est basé sur l’équilibre de forces et de moments, ce qui permet de retrouver le diagramme de contraintes de la section.
Dans le cas d’une section entièrement tendue, le béton n’apporte aucune résistance en traction. Les efforts des armatures sont les seuls à équilibrer les efforts extérieurs.
2.2.3 Génération du diagramme d’interaction
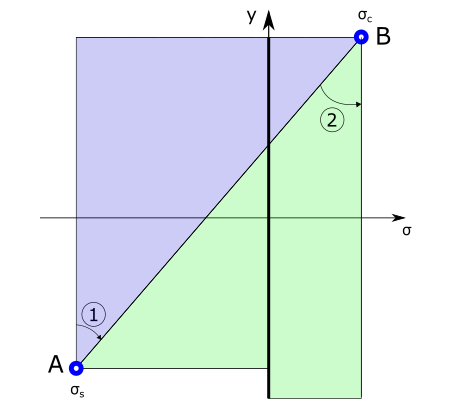
Le principe de génération des diagrammes d’interaction se base sur le balayage de tous les modes de flexion possibles de la section. Dans un but d’optimisation du travail de la section, ce balayage est fait en s’appuyant sur les contraintes limites de l’acier (pivot A) et du béton (pivot B) à l’ELS. Le diagramme de contraintes est homogénéisé pour tenir compte des modules de déformation différents de l’acier et du béton.
- Région 1 (pivot A) : elle consiste à maintenir la contrainte homogénéisée des aciers inférieurs égale à la contrainte limite de travail à l’ELS tout en faisant varier la contrainte de la fibre supérieure du béton entre la contrainte de travail de l’acier et la contrainte admissible du béton en compression à l’ELS. La résistance en traction du béton est négligée. L’axe neutre se déplace vers le centre au fur et à mesure. La section passe d’un état en traction pure vers entièrement en traction puis partiellement comprimée en partie supérieure de section.
- Région 2 (pivot B) : dans cette région la contrainte de la fibre supérieure du béton est égale à la contrainte admissible du béton à l’ELS tout en faisant diminuer la contrainte des aciers inférieurs. L’axe neutre continue à descendre vers la partie inférieure de la section. La section est entièrement comprimée dès que l’axe neutre sors en partie inférieure de la section.
2.2.4 Calcul des efforts résistants
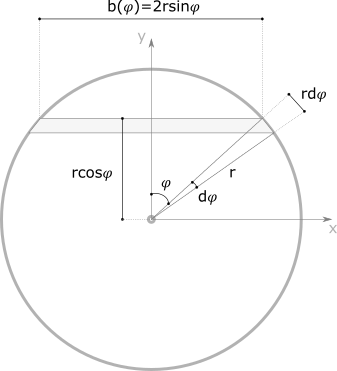
Chaque diagramme de contraintes homogénéisées est décrit par l’équation suivante : \[ \sigma_c(y)=ay+b \] \[ \sigma_c(\varphi)=aRcos\varphi+b \]
Où a représente la pente et b l’ordonnée à l’origine.
2.2.4.1 Effort résistant du béton
- Effort normal :
\[ N_c=\int_0^x\sigma_c(\varphi)b(\varphi)\operatorname dy \]
- Moment fléchissant :
\[ M_c=\int_0^x\sigma_c(\varphi)b(\varphi)y\operatorname dy \]
2.2.4.2 Effort résistant de l’acier
2.2.4.2.1 Répartition discrète des barres d’acier
Pour chaque barre de section \(A_i\) :
- Contrainte dans la barre “i” à partir du diagramme de contraintes de la section homogénéisée :
\[ \sigma_i=n \cdot \sigma_{homogénéisée} \]
Où n est le coefficient d’équivalence : \(n = E_s / E_c\)
- Force mobilisée dans la barre “i” :
\[ F_i=\sigma_i\cdot A_i \]
Force résultante sur l’ensemble des barres d’acier : \[ N_s=\sum_iF_i \]
2.2.4.2.2 Répartition continue et homogène de la section d’acier
- Diagramme de contrainte rectangulaire (palier plastique) :
\[ N_{s,rectangulaire}=2\int_{\varphi_1}^{\varphi_2}f_y\overline{a_s}r_s\operatorname d\varphi \]
\[ M_{s,rectangulaire}=2\int_{\varphi_1}^{\varphi_2}f_y\overline{a_s}r_sr_s\cos\varphi\operatorname d\varphi \]
- Diagramme de contrainte triangulaire (palier élastique) :
\[ N_{s,triangulaire}=2\int_{\varphi_2}^{\varphi_3}\sigma_{s,i}\left(\varphi\right)\overline{a_s}r_s\operatorname d\varphi \]
\[ M_{s,triangulaire}=2\int_{\varphi_2}^{\varphi_3}\sigma_{s,i}\left(\varphi\right)\overline{a_s}r_sr_s\cos(\varphi)\operatorname d\varphi \]
2.2.5 Calcul du taux de mobilisation de la résistance en flexion
Le taux de mobilisation de la résistance en flexion est le rapport entre le moment résistant et celui appliqué pour un même effort normal. Il est déduit du diagramme de déformation calculé pour la section examiné.
2.2.6 Contraintes limites à l’ELS exigées par la norme NF P 94-262
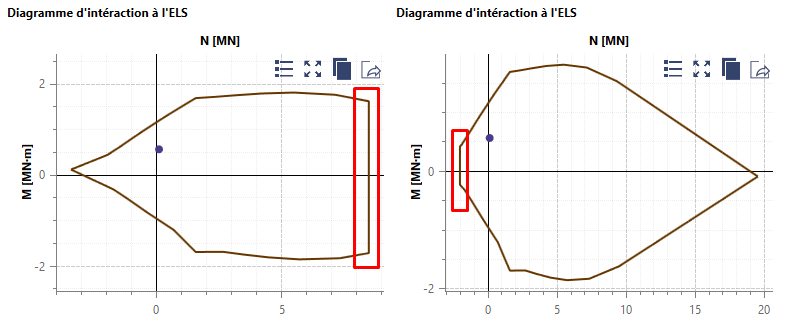
Scage permet de respecter les deux contraintes limites exigées par la norme NF P 94-262 :
- Contrainte moyenne de compression du béton à l’ELS Caractéristique = \(0.3k_3f_{ck}*\) (figure de gauche)
- Contrainte moyenne de traction à l’ELS Quasi-Permanent = \(600w_k\) (pour les éléments entièrement tendus) (figure de droite)
3 Section rectangulaire
Ce chapitre détaille le calcul d’une section rectangulaire en béton armé soumise à la flexion composée (ELS).
3.1 Notations
3.1.1 Géométrie
| Symbol | Unité | Description |
|---|---|---|
| b | m | Largeur de la section |
| h | m | Hauteur totale de la section |
| \(A_{s1}\) | m² | Section d’acier inférieure |
| \(A_{s2}\) | m² | Section d’acier supérieure |
| \(c_1\) | m | Distance entre le nu de la section et le centre de gravité des aciers inférieurs |
| \(c_2\) | m | Distance entre le nu de la section et le centre de gravité des aciers supérieurs |
| \(d_2\) | m | Position des armatures \(A_{s2}\) par rapport à la fibre inférieure de la section |
| \(v’\) | m | Position de G’ par rapport à la fibre inférieure de la section |
| G | - | Centre de gravité de la section rectangulaire |
| G’ | - | Centre de gravité de la section homogénéisée |
3.1.2 Efforts
| Symbol | Unité | Description |
|---|---|---|
| \(N_s\) | MN | Effort normal appliqué à G |
| \(M_s\) | MNm | Moment fléchissant appliqué à G |
| \(M\) | MNm | Moment fléchissant équivalent appliqué sur la fibre inférieure inférieure de la section |
| \(N\) | MN | Effort normal équivalent appliqué sur la fibre inférieure inférieure de la section |
| \(M'\) | MNm | Moment fléchissant équivalent appliqué à G’ |
| \(N'\) | MN | Effort normal équivalent appliqué à G’ |
| \(F_{s1}\) | MN | Effort repris par l’armatures tendue |
| \(F_{s2}\) | MN | Effort repris par l’armatures comprimée |
3.1.3 Contraintes
| Symbol | Unité | Description |
|---|---|---|
| \(\sigma_{s1}\) | MPa | Contrainte dans les aciers tendus |
| \(\sigma_{s2}\) | MPa | Contrainte dans les aciers comprimés |
| \(\sigma_c\) | MPa | Contrainte de compression dans le béton |
| \(f_{ck}\) | MPa | Contrainte admissible de compression du béton (valeur caractéristique) |
| \(f_{yd}\) | MPa | Contrainte admissible de l’acier (valeur de calcul) |
| \(f_{yk}\) | MPa | Contrainte admissible de l’acier (valeur caractéristique) |
3.2 Principe du calcul à l’ELS
Le principe de vérification d’une section à l’ELS est basé sur une analyse en contraintes.
Cette analyse en contraintes exige un calcul en section homogénéisée afin de considérer les différents modules de déformation de l’acier et du béton.
3.2.1 Hypothèses de calcul
Le calcul à l’ELS des sections en béton armé tient en compte des hypothèses suivantes :
- Hypothèse 1 : La résistance à la traction du béton est négligée.
- Hypothèse 2 : La résistance à la compression du béton est limitée à la contrainte admissible \(\overline{\sigma_c}\) à l’ELS.
- Hypothèse 3 : La résistance à la traction de l’acier est limitée à la contrainte admissible \(\overline{\sigma_s}\) à l’ELS.
Les lois de comportement du béton et de l’acier sont fournies dans le chapitre Matériaux de ce manuel.
3.2.2 Modes de fonctionnement de la section
En fonction du diagramme de contraintes généré par le torseur extérieur (\(M_s\), \(N_s\)), la section béton armé peut être en :
- Compression simple: effort normal de compression et moment nul.

- Partiellement comprimée: effort normal de compression et moment non nul.
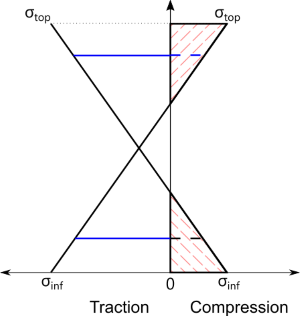
- Entièrement comprimée: effort normal de compression et moment non nul.
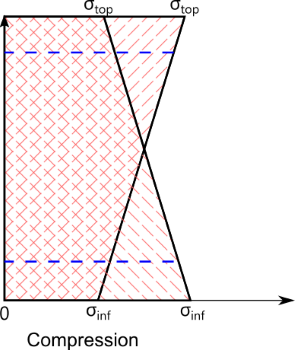
- Entièrement tendue: effort normal de traction et moment non nul.

3.3 Vérification de la section béton armé à l’ELS
La vérification de la section béton armé à l’ELS se réalise en homogénéisant la section afin de prendre en compte la présence de deux matériaux de rigidités différentes. L’équilibre de la section est basé sur l’équilibre de forces et de moments, ce qui permet de retrouver le diagramme de contraintes de la section.
Dans le cas d’une section entièrement tendue, le béton n’apporte aucune résistance en traction. Les efforts des armatures sont les seuls à équilibrer les efforts extérieurs.
3.4 Calcul des sections d’armature nécessaires
3.4.1 Partiellement et entièrement comprimée
Le principe de dimensionnement à l’ELS consiste à chercher la section minimale vérifiant l’équilibre de la section tout en garantissant le non dépassement des contraintes limites de chaque matériau.
3.4.2 Traction simple
En traction simple, la résistance en traction du béton est négligée. Seules les efforts des armatures compensent les efforts appliqués sur la section. La solution la plus économique consiste à garantir le centre de gravité des armatures au point d’application de l’effort normal.
Notons:
- \(e_{s1}\) distance entre le point d’application de l’effort normal et les armatures tendues
- \(e_{s2}\) distance entre le point d’application de l’effort normal et les armatures comprimées
Les des sections d’acier sont obtenues par équilibre de moments: \[ A_{s2}=\frac{Ne_{s1}}{\left(e_{s1}+e_{s2}\right)\sigma_{s2}} \]
\[ A_{s1}=\frac{Ne_{s2}}{\left(e_{s1}+e_{s2}\right)\sigma_{s1}} \]
Les contraintes dans les aciers sont considérées égales à la contrainte admissible à l’ELS.
4 Ouverture de fissures (\(w_k\))
\[ w_k=s_{r,max}\left(\varepsilon_{sm}-\varepsilon_{cm}\right) \]
| Terme | Unité | Description |
|---|---|---|
| \(w_k\) | mm | Ouverture de fissures |
| \(s_{r,max}\) | mm | Espacement maximal des fissures |
| \(\varepsilon_{sm}\) | - | Allongement moyen des armatures, sous la combinaison d’actions considérée, tenant compte de la contribution du béton tendu |
| \(\varepsilon_{cm}\) | - | Allongement moyen du béton entre les fissures |
\[ s_{r,max}=k_3c+0.425k_1k_2\frac{\phi_{eq}}{\rho_{p,eff}} \]
| Terme | Unité | Description |
|---|---|---|
| c | mm | Enrobage des armatures longitudinales |
| \(k_1\) | - | Coefficient fonction des propriétés adhérence des barres (0.8 pour les barres HA) |
| \(k_2\) | - | Coefficient tenant compte de a distribution des barre longitudinales \(k_2 = 0.5\) en flexion \(k_2 = 1\) en traction \(k_2=\frac{\varepsilon_1+\varepsilon_2}{2\varepsilon_1}\) en traction excentrée Avec \(\varepsilon_1\) le plus grandet et \(\varepsilon_2\) le plus faible des allongements relatifs des fibres extrêmes la section considérée, évalués sur la base d’une section fissuré. |
| \(k_3\) | - | Coefficient d’accompagnement de l’enrobage, égale à 3.4 |
| \(\phi_{eq}\) | mm | Diamètre équivalent des barres |
| \(\rho_{p,eff}\) | - | Ratio entre la section acier et la section de béton effective (\(A_s/A_{c,eff}\)) |
| \(A_{c,eff}\) | m² | Aire de béton entourant l’armature tendue sur une hauteur \(h_{c,ef}=min\left\{2.5\left(h-d\right)\;;\;\left(h-x\right)/3\;;\;h/2\right\}\) |
\[ \varepsilon_{sm}-\varepsilon_{cm}=max\left\{0.6\frac{\sigma_s}{E_s};\frac{\sigma_s+k_t{\displaystyle\frac{f_{ct,eff}}{\rho_{p,eff}}}\left(1+\alpha_e\rho_{p,eff}\right)}{E_s}\right\} \]
| Terme | Unité | Description |
|---|---|---|
| \(\sigma_s\) | MPa | Contrainte à l’ELS des armatures tendues, calculée en supposant la section fisurée |
| \(E_s\) | MPa | Module élastique de l’acier |
| \(f_{ct,eff}\) | MPa | Valeur moyenne de la résistance à la traction du béton effective au moment où les fissures sont censées se produire (\(f_{ct,eff}=f_{ctm}\)) |
| \(k_t\) | - | Coefficient tenant compte de la durée du chargement \(k_t=0.6\) pour un chargement de courte durée \(k_t=0.4\) pour un chargement de longue durée |
4.1 Cas particulier des sections circulaires
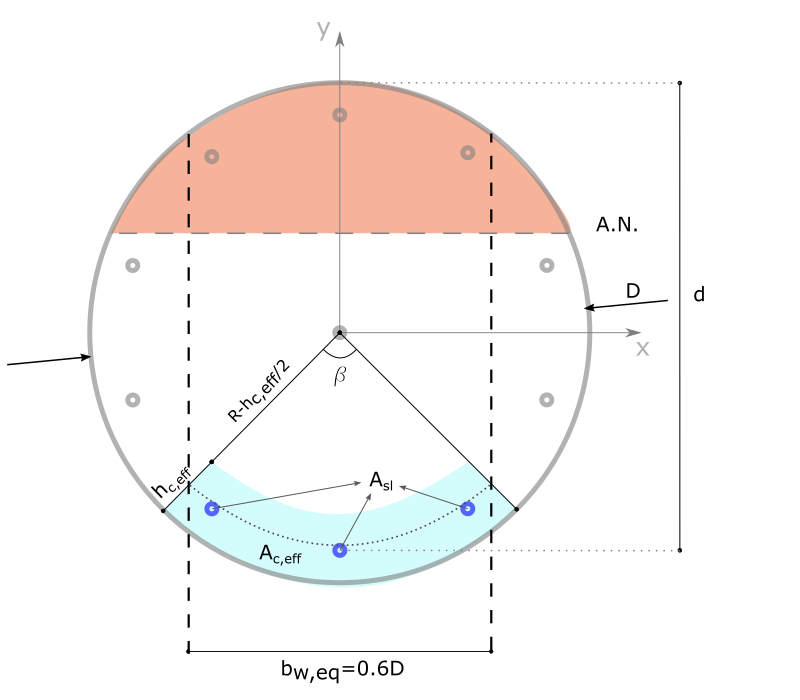
Le cas des sections circulaires n’est pas traité dans l’Eurocode 2 - Partie 1.1. Le Guide d’application de l’Eurocode 2 (FD P18-717) fait quelques propositions qui sont résumées ci-dessous dès lors qu’il y a au moins 6 barres longitudinales, ce qui es usuellement le cas dans les situations courantes.
Dans de cadre de la vérification de l’ouverture des fissures, la section circulaire est assimilée à une section rectangulaire équivalente des dimensions :
- Largeur : \(b_{w,eq}=0.6D\)
- Bras de levier : \(z=0.9d\)
avec \(D\) étant le diamètre du pieu et \(d\) la hauteur utile de la section.
La hauteur de béton comprimé est calculée avec la section circulaire.
Seules les armatures en traction à l’intérieur de cette section équivalente sont comptabilisées dans le terme \(A_{sl}\).
L’aire de béton entourant les armatures tendues (zone bleu clair) est assimilée à un segment de secteur circulaire d’angle central « beta » et de hauteur de hc,eff = min[ 2.5(D-d) ; (D-x)/3 ; D/2) ].