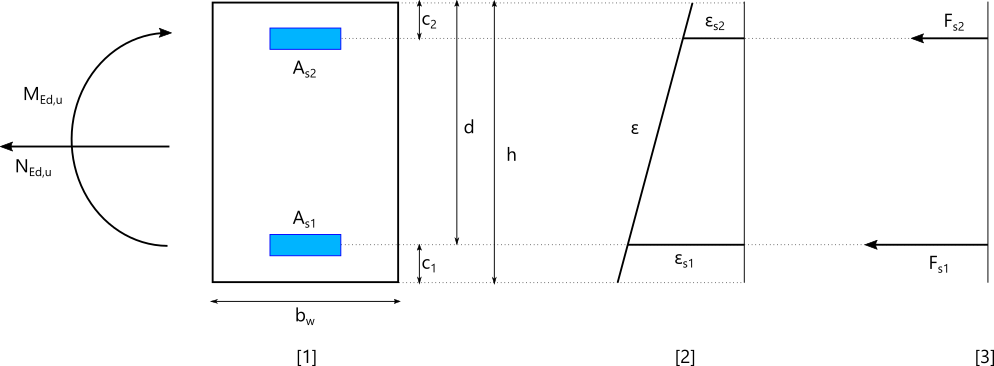Analyse à l’ELU
1 Introduction
Ce document détaille comment l’analyse à l’ELU est mené pour les sections circulaires et pour les sections rectangulaires en béton armé.
2 Section circulaire
Ce chapitre détaille le calcul d’une section circulaire en béton armé soumise à la flexion déviée (ELU).
2.1 Notations
2.1.2 Efforts
| Symbol | Unité | Description |
|---|---|---|
| \(N\) | MN | Effort normal appliqué sur la section béton armé |
| \(M_x\) | MNm | Moment fléchissant appliqué sur la section béton armé autour du semi-axe positive OX |
| \(M_y\) | MNm | Moment fléchissant appliqué sur la section béton armé autour du semi-axe positive OY |
| \(V_x\) | MN | Effort tranchant appliqué sur la section béton armé suivant le semi-axe positive OX |
| \(V_y\) | MN | Effort tranchant appliqué sur la section béton armé suivant le semi-axe positive OY |
La règle de la main droite s’applique :
- Un moment \(M_x>0\) comprime la fibre inférieure de la section (figure de gauche)
- Un moment \(M_y>0\) comprime la fibre à droite de la section (figure de droite)

2.1.3 Contraintes
| Symbol | Unité | Description |
|---|---|---|
| \(\sigma_{s,i}\) | MPa | Contrainte dans les aciers (barre “i”) |
| \(\sigma_c\) | MPa | Contrainte de compression dans le béton |
| \(f_{cd}\) | MPa | Contrainte admissible de compression du béton (valeur de calcul) |
| \(f_{ck}\) | MPa | Contrainte admissible de compression du béton (valeur caractéristique) |
| \(f_{yd}\) | MPa | Contrainte admissible de l’acier (valeur de calcul) |
| \(f_{yk}\) | MPa | Contrainte admissible de l’acier (valeur caractéristique) |
2.2 Principe de calcul à l’ELU
Le principe de calcul des sections circulaires (pieux) à l’ELU consiste à confronter le torseur résultant appliqué sur la section au diagramme d’interaction (N, M) de la section béton armé.
Ce diagramme d’interaction détermine le domaine admissible (zone intérieure du diagramme d’interaction, y compris la frontière) dans lequel se situent les couples (N, M) qui peuvent être repris par la section circulaire en béton armé.
2.2.1 Hypothèses de calcul
Le calcul à l’ELU des sections en béton armé tient en compte des hypothèses suivantes :
- Hypothèse 1: Les sections droites restent planes et il n’y a pas de glissement relatif entre les armatures et le béton. Le diagramme de déformation est donc linéaire.
- Hypothèse 2: La résistance à la traction du béton est négligée.

- Hypothèse 3: Le diagramme de déformations de la section correspond à un état-limite s’il passe par un des pivots A, B, C définis ci-dessous.
Les lois de comportement du béton et de l’acier sont fournis dans le chapitre Matériaux de ce manuel.
Les niveaux de déformation de calcul (\(\varepsilon\)) de chaque matériau, en particulier du béton (\(\varepsilon_c\)) et de l’acier (\(\varepsilon_s\)), sont définis par l’utilisateur et donc fixés avant de constituer les diagrammes d’interaction.
2.2.2 Génération du diagramme d’interaction
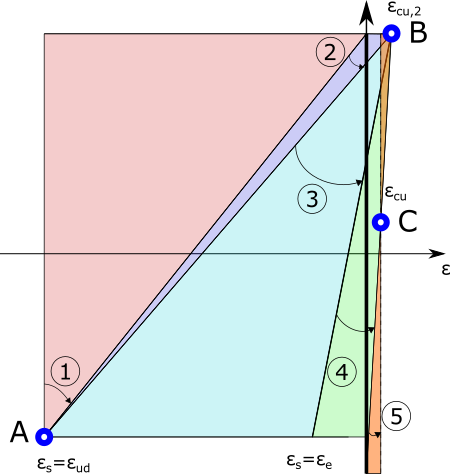
Le principe de génération des diagrammes d’interaction se base sur le balayage de tous les modes de flexion possibles de la section. Dans un but d’optimisation du travail de la section, ce balayage est fait en s’appuyant sur les pivots usuels A, B et C. L’éventail des régions possibles sont décrits comme suit :
- Région 1 (pivot A) : elle consiste à maintenir la déformation des aciers inférieurs à la valeur maximale \(\varepsilon_{ud}\) tout en faisant varier la déformation de la fibre supérieure de béton entre la valeur de la déformation limite de calcul de l’acier et une déformation nulle. La section reste complètement tendue dans cette région et l’apport du béton est donc négligé. L’effort résistant est uniquement apporté par la section d’acier. La limite gauche de la région correspond à un état de traction simple.
- Région 2 (pivot A) : en gardant la déformation dans les aciers inférieurs fixée à \(\varepsilon_{ud}\), la déformation de la fibre supérieure du béton augmente depuis sa valeur nulle jusqu’à \(\varepsilon_{cu,2}\). Le section commence à être comprimée et l’axe neutre commence à se déplacer vers le centre de la section. La courbure de la section devient maximale pour le diagramme passant par \(\varepsilon_s=\varepsilon_{ud}\) et \(\varepsilon_c=\varepsilon_{cu,2}\). La section est partiellement comprimée en partie supérieure.
- Région 3 (pivot B) : en fixant la valeur de la déformation supérieure à \(\varepsilon_{cu,2}\), la déformation des aciers inférieurs commence à diminuer progressivement jusqu’à la limite élastique \(\varepsilon_s=\varepsilon_{s}=f_{yd}/E_s\). L’axe neutre continue à descendre vers le centre de la section, ce qui provoque une augmentation de la hauteur comprimée et la courbure diminue. La section est partiellement comprimée en partie supérieure.
- Région 4 (pivot B) : la déformation de la fibre supérieure du béton restant fixée à \(\varepsilon_{cu,2}\), la déformation des aciers inférieurs continue à diminuer en rentrant même dans un mode de travail de compression jusqu’à ce que la déformation de la fibre inférieure du béton s’annule. L’axe neutre atteint le niveau inférieure de la section et la courbure continue à diminuer. La section devient comprimée avec peu d’excentricité.
- Région 5 (pivot C) : dans cette région, le diagramme de déformations tourne autour du pivot C situé au niveau de la fibre qui suit une déformation \(\varepsilon_c=\varepsilon_{cu}\) à la fin de la région précédente, jusqu’à atteindre une déformation uniforme égale à \(\varepsilon_c=\varepsilon_{cu}\) en fibre supérieure et inférieure du béton. La section est complètement comprimée, le dernier état correspondant à la compression simple.
2.2.3 Calcul des efforts résistants
L’effort résistant de la section est calculé pour chaque diagramme de déformation. Il est composé d’une partie provenant de l’acier et une autre partie provenant du béton (uniquement s’il est comprimé, l’apport en traction est négligé).
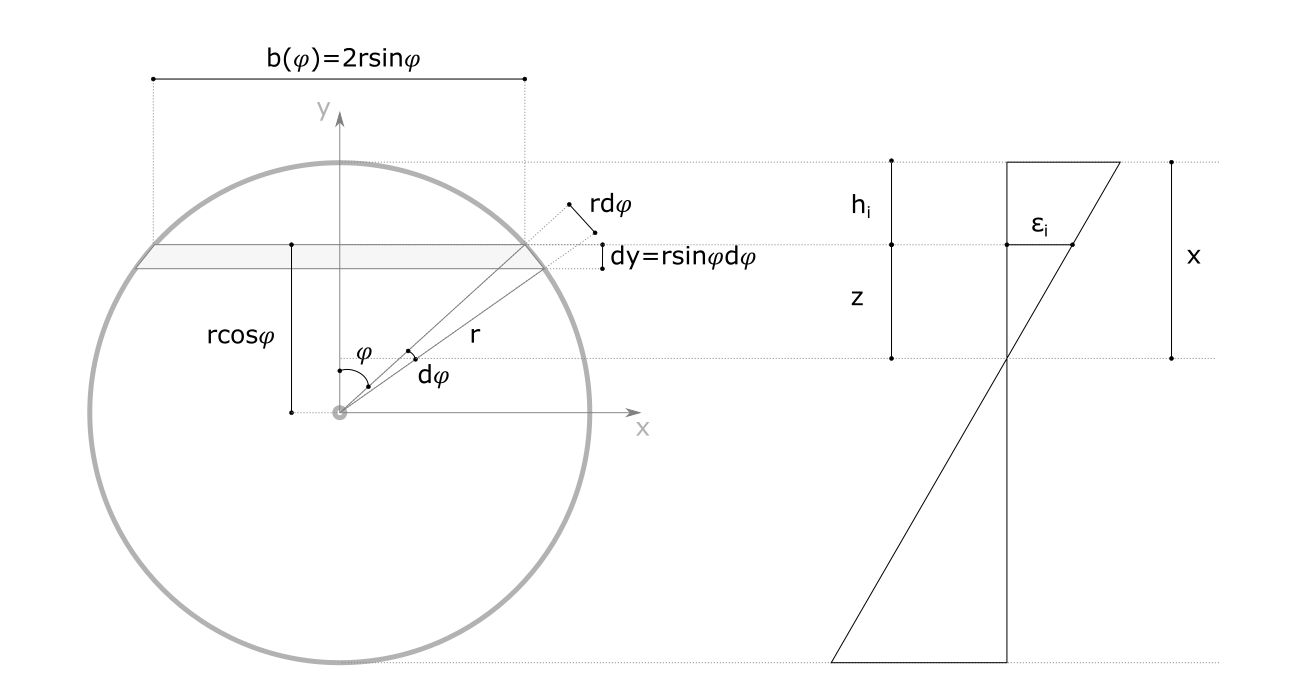
2.2.3.1 Effort résistant du béton
L’effort apporté par le béton est comptabilisé sur la base de la loi parabole-rectangle. \[ \left\{\begin{array}{lc}\sigma_c=\left(\varepsilon_c-0.25\varepsilon_c^2\right)f_c&0<\varepsilon_c<2‰\\\sigma_c=f_c&2‰\leq\varepsilon_c\leq3.5‰\end{array}\right. \]
Efforts résistants sur la partie “rectangle” :
Effort normal résistant : \[ N_{c1}=\int_0^xf_cb\left(\varphi\right)\operatorname dy \]
Moment résistant : \[ M_{c1}=\int_0^xf_cb\left(\varphi\right)r\cos\varphi\operatorname dy \]
Efforts résistants sur la partie “parabole” :
Effort normal résistant : \[ N_{c2}=\int_0^x\sigma_{ci}\left(\varphi\right)b\left(\varphi\right)\operatorname dy \]
Moment résistant :
\[ M_{c2}=\int_{x_2}^{x_3}\sigma_{ci}\left(\varphi\right)b\left(\varphi\right)r\cos\left(\varphi\right)\operatorname dy \]
2.2.3.2 Effort résistant de l’acier
L’effort apporté par l’acier est comptabilisé sur la base de la loi bilinéaire. \[ \left\{\begin{array}{lc}\sigma_s=E_s\varepsilon_s&0<\varepsilon_s<\varepsilon_e\\\sigma_s=\sigma_y&\varepsilon_e<\varepsilon_s\leq\varepsilon_{ud}\end{array}\right. \]
2.2.3.2.1 Répartition discrète des barres d’acier
Pour chaque barre de section \(A_i\) :
- Contrainte dans la barre “i” à partir du diagramme de déformation :
\[ \sigma_i=\sigma(\varepsilon_i) \]
- Force mobilisée dans la barre “i” :
\[ F_i=\sigma_i\cdot A_i \]
- Force résultante sur l’ensemble des barres d’acier :
\[ N_s=\sum_iF_i \]
2.2.3.2.2 Répartition continue et homogène de la section d’acier

\(\overline{a_s}\) représente la densité linéaire de section d’acier
- Diagramme rectangulaire de contraintes (zone plastique) entre \(\varphi_1\) et \(\varphi_2\) :
\[ N_{s,rectangulaire}=2\int_{\varphi_1}^{\varphi_2}f_y\overline{a_s}r_s\operatorname d\varphi \]
\[ M_{s,rectangulaire}=2\int_{\varphi_1}^{\varphi_2}f_y\overline{a_s}r_sr_s\cos\varphi\operatorname d\varphi \]
- Diagramme triangulaire de contraintes (zone élastique) entre \(\varphi_2\) et \(\varphi_3\) :
\[ N_{s,triangulaire}=2\int_{\varphi_2}^{\varphi_3}\sigma_{s,i}\left(\varphi\right)\overline{a_s}r_s\operatorname d\varphi \]
\[ M_{s,triangulaire}=2\int_{\varphi_2}^{\varphi_3}\sigma_{s,i}\left(\varphi\right)\overline{a_s}r_sr_s\cos(\varphi)\operatorname d\varphi \]
- Diagramme rectangulaire de contraintes (zone plastique) entre \(\varphi_3\) et \(\varphi_4\) : formulation identique au premier cas entre \(\varphi_1\) et \(\varphi_2\).
3 Section rectangulaire
Ce chapitre détaille le calcul d’une section rectangulaire en béton armé soumise à la flexion composée (ELU).
3.1 Notations
3.1.1 Géométrie
| Symbol | Unité | Description |
|---|---|---|
| b | m | Largeur de la section |
| h | m | Hauteur totale de la section |
| d | m | Hauteur effective de la section |
| \(c_1\) | m | Distance entre le nu de la section et le centre de gravité des aciers tendus |
| \(c_2\) | m | Distance entre le nu de la section et le centre de gravité des aciers comprimés |
| x | m | Position de l’axe neutre depuis la fibre la plus comprimée |
| \(A_{s1}\) | m² | Section d’acier tendue |
| \(A_{s2}\) | m² | Section d’acier comprimée |
| \(z_R\) | m | Bras de levier associé à \(M_R\) |
3.1.2 Efforts
| Symbol | Unité | Description |
|---|---|---|
| \(N\) | MN | Effort normal appliqué sur la section béton armé |
| \(M\) | MNm | Moment fléchissant appliqué sur la section béton armé (au niveau de l’armature inf.) |
| \(M_c\) | MNm | Moment fléchissant reprit par le béton seul |
| \(N_c\) | MN | Effort normal repris par le béton seul |
| \(F_{s1}\) | MN | Effort repris par l’armatures tendue |
| \(F_{s2}\) | MN | Effort repris par l’armatures comprimée |
| \(M_R\) | MNm | Moment résistant de la section béton armé au-delà duquel il convient de disposer une armature comprimée pour faire travailler correctement l’armature tendue |
| \(N_R\) | MN | Effort normal repris par le béton associé à \(M_R\) |
3.1.3 Contraintes
| Symbol | Unité | Description |
|---|---|---|
| \(\sigma_{s1}\) | MPa | Contrainte dans les aciers tendus |
| \(\sigma_{s2}\) | MPa | Contrainte dans les aciers comprimés |
| \(\sigma_c\) | MPa | Contrainte de compression dans le béton |
| \(f_{cd}\) | MPa | Contrainte admissible de compression du béton (valeur de calcul) |
| \(f_{ck}\) | MPa | Contrainte admissible de compression du béton (valeur caractéristique) |
| \(f_{yd}\) | MPa | Contrainte admissible de l’acier (valeur de calcul) |
| \(f_{yk}\) | MPa | Contrainte admissible de l’acier (valeur caractéristique) |
3.2 Principe du calcul à l’ELU
Le principe de dimensionnement d’une section à l’ELU est basé sur une analyse en déformations.
3.2.1 Hypothèses de calcul
Le calcul à l’ELU des sections en béton armé tient en compte des hypothèses suivantes :
- Hypothèse 1: Les sections droites restent planes et il n’y a pas de glissement relatif entre les armatures et le béton. Le diagramme de déformation est donc linéaire.

- Hypothèse 2: La résistance à la traction du béton est négligée.

- Hypothèse 3: Le diagramme de déformations de la section correspond à un état-limite s’il passe par un des pivots A, B, C définis ci-dessous.
Les lois de comportement du béton et de l’acier sont fournis dans le chapitre Matériaux de ce manuel.
3.2.2 Modes de fonctionnement de la section
Le dimensionnement optimisé d’une section béton armé exige un diagramme de déformations qui passe par une déformation limite, soit du béton, soit de l’acier. Ces déformations limites sont caractérisées par les pivots.
Trois pivots permettent de différencier le mode de fonctionnement de la section:
- Pivot A: la déformation des aciers tendus correspond à la déformation maximale admissible de l’acier (\(\varepsilon_{ud}\))
- Pivot B: la déformation de la fibre de béton la plus comprimée correspond à la déformation maximale admissible (\(\varepsilon_{cu}\))
- Pivot C: la déformation du béton est considérée étant égale à la déformation élastique maximale admissible (\(\varepsilon_{ce}\)) sur la hauteur comprimée du béton.
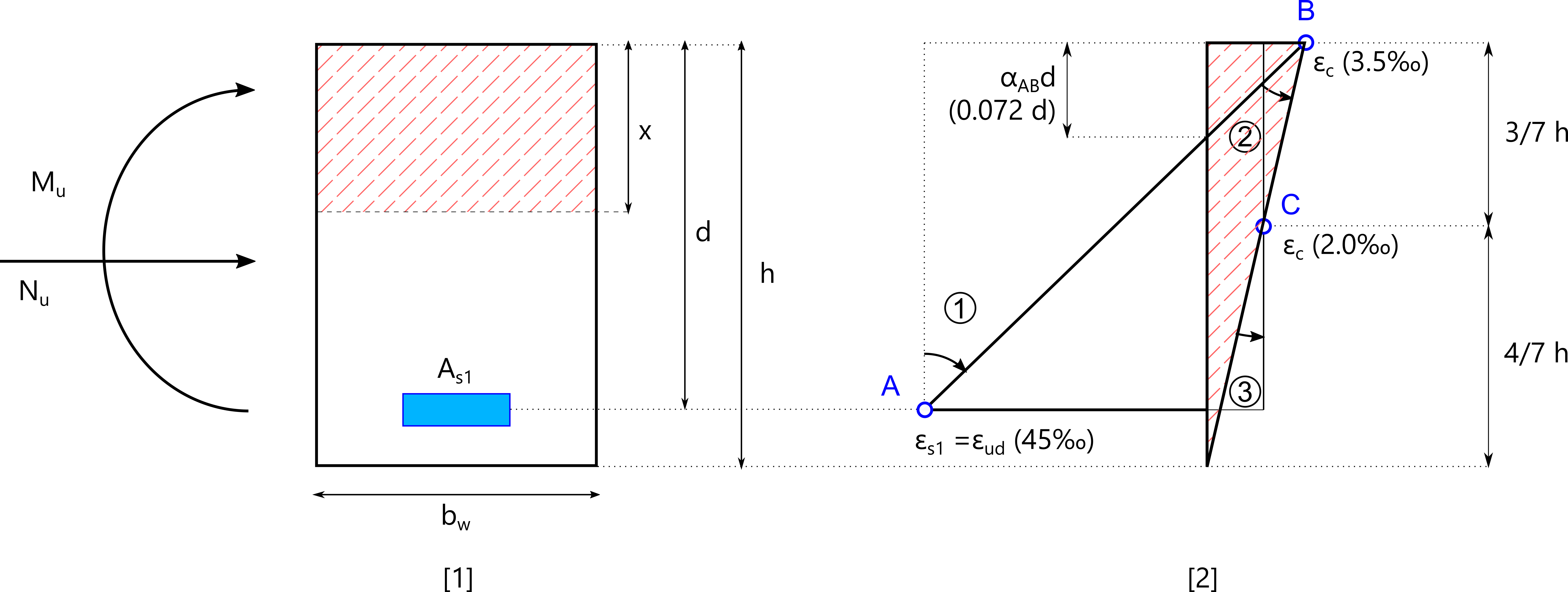
Notons \(x\) la position de l’axe neutre depuis la fibre la plus comprimée.
Si le diagramme passe au même temps par les pivots A et B, alors: \[ x=\frac{\varepsilon_{cu}}{\varepsilon_{cu}+\varepsilon_{ud}}d=\frac{3.5‰}{3.5‰+45‰}d=0.072d \] Les diagramme de déformations de la section peut se retrouver dans un des trois domaines définis par les pivots:
- Domaine 1 : $0<x<0.072d $ → Section partiellement comprimée
- Domaine 2 : \(0.072d\leq x<h\) → Section partiellement comprimée
- Domaine 3 : $hx $ → Section entièrement comprimée
3.2.2.1 Section partiellement comprimée
En fonction de la position de l’axe neutre, 2 cas sont possibles :
- \(0.072d\leq x<h\)
Le diagramme de déformations de la section se trouve dans le domaine 2.

Le raccourcissement de la fibre la plus comprimée est \(\varepsilon_c=3.5‰\), ce qui correspond à une contrainte égale à \(f_{cd}\).
Le diagramme de contraintes comporte deux parties: une partie droite sur une hauteur égale à \(3/7x\) et une partie de parabole sur une hauteur égale à \(4/7x\).
Cette répartition des hauteurs provient de l’allure de la loi de comportement du béton. Le diagramme de déformations étant linéaire sur la hauteur comprimée:
- Les déformations du béton supérieures à 2‰ engendrent une contrainte égale à \(f_{cd}\).
- Les déformations du béton inférieures à 2‰ suivent une distribution parabolique de contraintes variant entre 0 et \(f_{cd}\).
2‰ correspond à la déformation maximale du domaine élastique, soit \(2‰/3.5‰=4/7\) de la hauteur comprimée.
Effort normal et moment repris par le béton : \[ N_c=0.81bxf_{cd} \label{Nc} \]
\[ M_c=0.81bxf_{cd}(h-0.416x) \label{Mc} \]
La relation entre \(M_c\) et \(N_c\) peut être déduite des expressions précédentes: \[ \eqref{Nc},\eqref{Mc} → M_c=N_c(h-0.514\frac{N_c}{bf_{cd}}) \label{McNcRelation} \]
- \(0<x<0.072d\)
Le diagramme de déformations de la section se trouve dans le domaine 1.
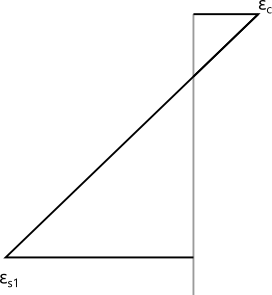
Le raccourcissement de la fibre la plus comprimée est inférieur à 3.5 ‰ et le diagramme peut avoir l’un des deux formes indiquées ci-dessous.

Dans ce cas :
Pour une valeur de x comprise entre 0 et 0.072d, la valeur du bras de levier des efforts \(z=M_c/N_c\) est comprise entre:
\(z=d\) pour \(x=0\)
\(z=0.97d\) pour \(x=0.072d\)
La section de béton étant surabondante, il est inutile d’établir une armature comprimée.
Nous constatons que la variation relative du bras de levier est très faible et qu’il n’est pas nécessaire d’évaluer x avec grande précision, ce qui autorise l’emploi des relations \(\eqref{Nc}\), \(\eqref{Mc}\) et \(\eqref{McNcRelation}\) comme dans le domaine 2.
3.2.2.2 Section entièrement comprimée
Le diagramme de déformations de la section se trouve dans le domaine 3 et passe par le pivot C.
Le diagramme de contraintes est composé d’une droite sur une hauteur totale égale à \(3/7h\) et d’une parabole sur une hauteur total égale à \(4/7h\).

L’état d’équilibre de la section est obtenu à partir de l’équilibre de forces et moments, permettant d’obtenir le diagramme de déformations associé au torseur appliqué.
3.3 Calcul des sections d’armature nécessaires
La formulation retenue dans Scage consiste à proposer une solution voisine de la solution la plus économique. Nous n’établirons pas, en principe, une armature si sa déformation relative est inférieure à la déformation élastique \(\varepsilon_e\) . Si cela n’est pas possible, l’effort repris par ces armatures sera minimisé.
3.3.1 Section partiellement comprimée
Une section est partiellement comprimée si les efforts N et M (calculé au niveau de l’armature inférieure) aboutissent à un diagramme de déformations composé d’une partie en compression et en traction.
Notons \(M_R\) le moment équilibré par le béton.
- \(M\leq M_R\)
Dans ce cas, pas nécessité d’armature comprimée car le moment est équilibré par le béton tout seul.
L’armature inférieure est tendue avec un allongement supérieur à \(\varepsilon_e\), donc bien utilisée.

Le calcul d’équilibre permet de retrouver la section d’acier nécessaire en partie inférieure.
- \(M_R< M\)
Dans ce cas, il convient de prévoir une armature comprimée pour garantir que l’armature tendue est bien utilisée et que la contrainte de béton n’excède pas la contrainte admissible.

Le calcul d’équilibre conduit aux sections d’acier nécessaires de chaque côté pour garantir que les efforts agissants sont correctement repris.
3.3.2 Section entièrement comprimée
Une section est entièrement comprimée si les efforts N et M (calculé au niveau de l’armature inférieure) engendrent un diagramme de déformations purement en compression (aucune zone en traction). Dans ce cas là, le diagramme de déformations passe par le point C.
Si la section comporte deux armatures, l’armature inférieure est la moins bien utilisée des deux puisqu’elle a le plus faible raccourcissement relatif. De ce fait, on cherchera à équilibrer les efforts sans établir d’armature inférieure.
Le calcul d’équilibre conduit aux sections d’acier nécessaires pour garantir que les efforts agissants sont correctement repris par les aciers et le béton.
3.3.3 Section en traction simple
La résistance en traction du béton est négligée. Seules les efforts des armatures compensent les efforts appliqués sur la section. La solution la plus économique consiste à garantir le centre de gravité des armatures au point d’application de l’effort normal.
Notons:
- \(e_{s1}\) distance entre le point d’application de l’effort normal et les armatures tendues
- \(e_{s2}\) distance entre le point d’application de l’effort normal et les armatures comprimées
Les des sections d’acier sont obtenues par équilibre de moments: \[ A_{s2}=\frac{Ne_{s1}}{\left(e_{s1}+e_{s2}\right)\sigma_{s2}} \]
\[ A_{s1}=\frac{Ne_{s2}}{\left(e_{s1}+e_{s2}\right)\sigma_{s1}} \]
Les contraintes dans les aciers sont considérées égales à \(\sigma=\sigma(\varepsilon_{ud})\).