Dimensionnement des armatures transversales
2 Notations
| Symbol | Unité | Description |
|---|---|---|
| \(V_{Ed}\) | kN | Effort tranchant agissant |
| \(V_{Rd,c}\) | kN | Effort tranchant résistant de calcul pour un élément sans armatures d’effort tranchant |
| \(V_{Rd,s}\) | kN | Valeur de calcul de l’effort tranchant équilibré par des armatures d’effort tranchant à l’état limite ultime |
| \(V_{Rd,max}\) | kN | Valeur de calcul de l’effort tranchant maximal que peut supporter un élément, avant l’écrasement des bielles de béton |
3 Efforts de calcul
3.1 Éléments dépourvus d’armature transversale
- Effort tranchant résistant de calcul pour un élément sans armatures d’effort tranchant :
\[ V_{Rd,c}=max\left\{\begin{array}{l}V_{Rd,c1}=\left[C_{Rd,c}k\sqrt[3]{100\rho_1f_{ck}}+k_1\sigma_{cp}\right]b_wd\\V_{Rd,c2}=\left[v_{min}+k_1\sigma_{cp}\right]b_wd\end{array}\right. \]
Avec :
\[ C_{Rd,c}=\frac{0.18}{\gamma_c} \]
- Pourcentage d’armatures longitudinales : \[ \rho_1=\frac{A_{sl}}{b_wd}\not>2‰ \]
Avec :
\[ k=min\left\{2;\;1+\sqrt{\frac{0.2\;m}d}\right\} \]
- Contrainte de compression du béton : \[ \sigma_{cp}=\frac{N_{Ed}}{A_c}\leq0.2f_{cd} \]
Avec :
\[ v_{min}=\frac{0.053}{\gamma_c}k^{3/2}\sqrt{f_{ck}} \]
\[ k_1=0.15 \]
Aucune armature transversale n’est requise si \(V_{Ed}\leq V_{Rd,c}\).
3.2 Effort tranchant maximal
Même si aucune armature transversale est requise, la condition suivante doit être respectée : \[ V_{Ed}\leq V_{Rd,max} \] Où \(V_{Rd,max}\) est la valeur de calcul de l’effort tranchant maximal que peut supporter un élément, avant l’écrasement des bielles de béton :
\[ V_{Rd,max}=\alpha_{cw}v_1f_{cd}b_wz\frac1{\tan\theta+co\tan\theta} \] Avec :
\[ z=0.9d \]
\[ \alpha_{cw}=\left\{\begin{array}{lc}0<\sigma_{cp}<0.25f_{cd}&\alpha_{cw}=1+\frac{\sigma_{cp}}{f_{cd}}\\\begin{array}{l}0.25f_{cd}<\sigma_{cp}<0.5f_{cd}\\0.5f_{cd}<\sigma_{cp}<f_{cd}\end{array}&\begin{array}{l}\alpha_{cw}=1.25\\\alpha_{cw}=2.5\left(1-\frac{\sigma_{cp}}{f_{cd}}\right)\end{array}\end{array}\right. \]
3.3 Force de traction dans l’armature longitudinale
La force de traction dans l’armature longitudinale est calculée à partir de l’expression suivante, il convient de veiller à ne pas dépasser l’effort à reprendre par les armatures. \[ F_{td}=\frac{M_{Ed}}z+\frac12V_{Ed}\left(co\tan\theta-co\tan\alpha\right)\leq\frac{M_{Ed,max}}z \]
4 Calcul des armatures transversales
Lorsque \(V_{Ed}>V_{Rd,c}\), les armatures transversales sont requises.
Il convient de choisir une inclinaison des bielles comprise entre \(1.0\leq co\tan\theta\leq2.5\)
4.1 Vérification de la compression des bielles de béton
Il convient de vérifier que l’effort de compression des bielles de béton n’est as dépassé :
\[ V_{Ed}\leq V_{Rd,max}=b_wzv_1f_{cd}\frac{co\tan\theta+co\tan\alpha}{1+\left(co\tan\theta\right)^2} \] Avec :
- \(z=0.9d\)
- \(v_1=0.6\left(1-\frac{f_{ck}}{250}\right)\)
4.2 Calcul des armatures d’effort tranchant
L’effort repris par les armatures transversales est calculé comme suit :
\[ V_{Rd,s}=\rho_wf_{ywd}\sin^2\alpha\left(co\tan\theta+co\tan\alpha\right)b_wz=\frac{A_{sw}}{sb_w\sin\alpha}f_{ywd}\sin^2\alpha\left(co\tan\theta+co\tan\alpha\right)b_wz \] L’effort repris par les armatures transversale doit être égalisé à l’effort tranchant de calcul pour retrouver la section transversale d’acier nécessaire à reprendre l’effort tranchant agissant \(V_{Ed}\). \[ \frac{A_{sw}}s=\frac{V_{Ed}}{zf_{ywd}\left(co\tan\theta+co\tan\alpha\right)\sin\alpha} \]
4.3 Pourcentage minimal d’armatures transversales
Le pourcentage d’armatures transversales se calcule comme suit :
\[ \rho_w=\frac{A_{sw}}{sb_w\sin\alpha} \] Où : * \(A_{sw}\) est la section d’armatures transversales à une section donnée * \(s\) est l’espacement des armatures transversales * \(b_w\) est la largeur de la section * \(\alpha\) est l’inclinaison des armatures transversales par rapport aux armatures longitudinales.
Même lorsqu’aucune armatures d’effort tranchant n’est requise, un ferraillage transversal minimal est à prévoir. Le pourcentage d’armatures transversales minimales se calcule comme suit :
\[ \rho_{w,min}=0.08\frac{\sqrt{f_{ck}}}{f_{yk}} \]
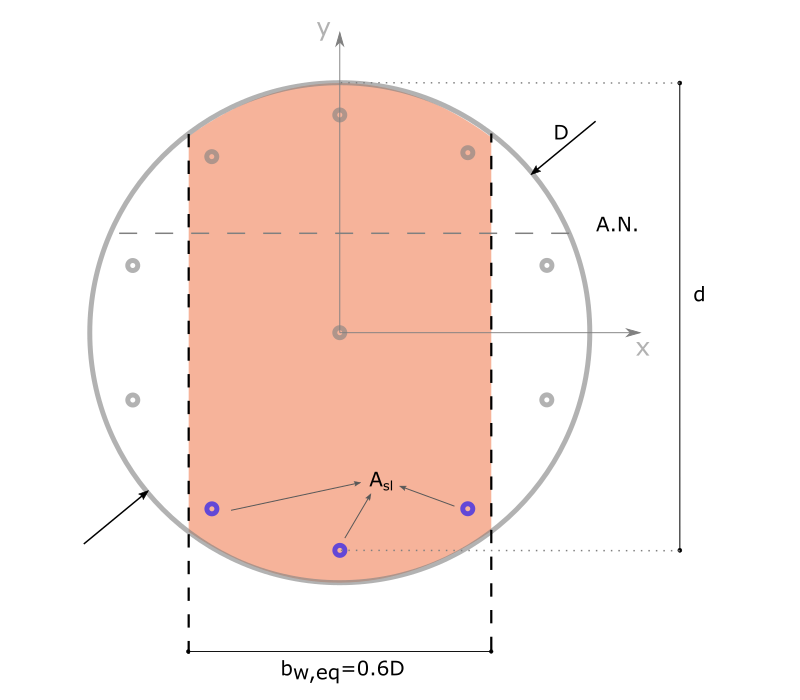
5 Cas particulier des sections circulaires (pieux)
Le cas des sections circulaires n’est pas traité dans l’Eurocode 2 - Partie 1.1. Le Guide d’application de l’Eurocode 2 (FD P18-717) fait quelques propositions qui sont résumées ci-dessous dès lors qu’il y a au moins 6 barres longitudinales, ce qui es usuellement le cas dans les situations courantes.
Dans de cadre de la vérification de l’effort tranchant et du calcul des armatures transversales, la section circulaire est assimilée à une section rectangulaire équivalente des dimensions :
- Largeur : \(b_{w,eq}=0.6D\)
- Bras de levier : \(z=0.9d\)
avec \(D\) étant le diamètre du pieu et \(d\) la hauteur utile de la section.
Seules les armatures en traction à l’intérieur de cette section équivalente sont comptabilisées dans le terme \(A_{sl}\).